오늘은 Loss function에 대하여 학습을 진행할 것이다. Loss function으로 미분이 가능하게 만들어, 학습에 판단 지표로 만든다는 것은 알겠는데, 각각 무슨차이인지 몰랐다. 이번 학습을 통해 조금 더 loss function에 가까워졌다. 추가로 미니 배치와 배깅 알고리즘을 정리하며 이해의 폭을 넓힐 예정이다.
전체 목차
- MAE vs MSE vs RMSE
- Cross entropy vs Negatinve log likehood loss
- 미니 배치 vs 배깅 알고리즘 정리
세부 목차
- 최대 우도법?
- Negative log likelihood
- Cross entropy
- Negative log likelihood vs Cross entropy
| 최대 우도법(likelihood) |
복잡한 수식보다 핵심적인 키워드를 알려주겠다. 최대 우도법의 핵심은 어떠한 데이터가 주어졌을때, 확률 밀도 함수를 모른다는 가정하에 가장 잘 맞는 확률 밀도 함수를 추정하는 방법이다. 즉, 데이터에 가장 잘맞는 (모델, 추정치) 계산법.
예시로 회귀의 경우를 설명하겠다.
ex) y(종속 변수) = w(회기 계수)x(독립 변수)
w: 추정하는 값(추정치, 파라미터)
y: 종속변수(모델)

즉 위에서 파란색 점은 이미 주어진 데이터, 즉 실제값이다. 예측값의 모델을 만들때, 주어진 파란색의 점들을 가장 잘 표현 할 수 있는 선을 만들어야 하는데, 이것이 우도의 기본 개념인 것이다.
최대 우도법은 클 수록 좋은 값이 되는데, 클수록 주어진 데이터를 잘 표현하는 모델이 만들어지기 때문이다.

주어진 이미지를 보고 밑에 점과 가장 잘맞는 확률밀도함수는 무엇일까?
주황색
직접 보니까 직관적인 이해는 할 수 있지만, 어떻게 수학적으로 표현을 해야할까?

위의 점에서 떨어진 각각의 거리를 구한후 곱해주는 방식으로 구하면 된다. 이런 방식을 사용하여 파란색과 주황색의 각 데이터 별 떨어진 거리를 구하고 곱한 값이 가장 큰 값을 확률로 표현한 것. 그것이 최대 우도법의 가장 기본적인 개념이다.
(당연히 주황색이 밀집된 부분과 밀도 함수의 중앙과 거리가 가장 멀어, 우도가 가장 큼.)
| 확률과의 차이 |
확률과 우도의 방식을 조건부 확률로 나타내면
확률: p(data | model)
우도: p(model | data)
쉽게 말해
확률: 모델과 추정치 -> 데이터
우도: 데이터 -> 모델과 추정치
우도는 데이터를 보고(원인)-> 모델(결과)
확률은 모델과 추정치(원인) -> 데이터(결과)의 형식이다.
ex) 동전 3번 던질때의 확률
(1/2)^3(모델) -> 실제 3번 던졌을 때 나오는 값(데이터)
인과관계가 반대라고 생각하면 이해하기 쉬울 거 같다.
| 우도의 log 사용 |
수식을 보자

수식을 유도하는 것은 나도 모른다. 하지만 저것이 의미하는 것이 각 포인트별 떨어진 거리의 곱인 것은 안다. 즉, 어떠한 데이터를 보고 최적의 파라미터 (모델과, 가중치)를 추정하는 것이다.
보통 우도를 사용할때, log를 씌워서 사용하는데 그 이유는
1. 계산 용이성
2. 직관적인 이해가능
3. 확률의 곱으로 인한 underflow 방지
log를 사용하면, 거리의 곱셈을 덧셈으로 표현할 수 있고, 지수를 곱으로 표현할 수 있는 장점이 있다. 또한 여러개의 확률(우도 값) 을 곱하다보면, 파이썬의 경우 underflow가 발생하는데 log로 인해 덧셈으로 변환하여 방지할 수 있다.
간단하게 저 식의 구현을 이해해보자.
보통 Cross entropy나 log likelihood의 경우는 분류에서 많이 사용된다.
직관적으로 분류는 2가지가 있는데
1. binary (이진 분류)
2. Multiclass(다범주 분류)
이해하기 쉽게 먼저 이진 분류의 예시로 설명하겠다.
binary
binary classification의 경우. 보통 sigmoid 함수를 활성화 함수로, 분류의 값이 0 or 1로 만드는 것이다.
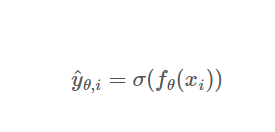
쉽게 예측 값을 앞으로 y_pred로 쓰겠다. y_pred는 모델이 예측한 값이 정답(positive)일 확률의 식이다. 주어진 데이터에서 우도(likelihood)값이 최대화하는 파라미터 θ 를 구하는 것이다.
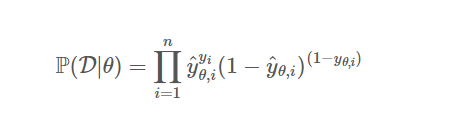
정답의 경우의 수 즉, 나올 수 있는 정답 y =0 or 1이다.
y(i)의 경우는 i번째에서 y의 값이다. 경우의 수를 따져 보자.
- y(i) = 0
- y(i) = 1
두 가지로 봐보자.
첫 번째 경우는
y(i) = 0
앞쪽에 y_pred의 0승으로 1이된다. (1 - y_pred) ^ (1-y(i))에서 지수 쪽 1-0= 1이니,
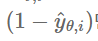
위의 식만 남게 된다. 즉 예측 값이 0 (정답)에 가까울 수록, 우도가 커진다. (1에 가까워진다.) 이렇게 각 데이터 별로 나온 모든 확률값들을 곱해주는 방식으로 전개 된다.
두 번째 경우는
y(i) = 1
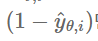
위의 식이 1이 된다. 즉,
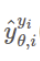
y_pred가 1 즉 정답에 가까울 수록 동일하게 우도가 커지는 방식이다.
log 변환
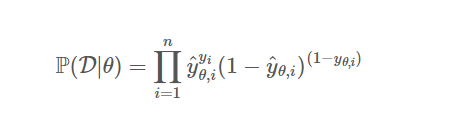
위의 식은 곱으로 이루어져 있어 로그 변환시 덧셈으로 연결할 수 있다.
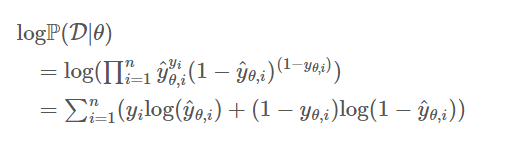

영상을 보면, 대략 이해가 가능하다.
1. sigmoid로 인한 이진 분류 0 or 1
2. log 함수를 적용
3. label에 맞는 값 선택
4. 각 데이터 log likelihood값 합
최종적으로 우리는 이진 분류에서 손실 함수를 사용할 때,
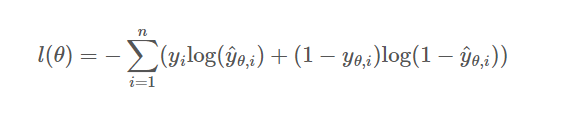
Negative(음의 값)으로 변환하여 사용하는데, 그 이유는 손실 함수의 미분, 경사하강법 사용시 loss 함수를 작아지는 방향으로 정의해야하기 때문이다.
log 함수는 항상 증가하는 함수이기 때문에, -를 취해 사용해도 괜찮다.
요약
- likelihood를 최대화 = log likelihood를 최대화
- likelihood를 최대화 = Negative likelihood 를 최소화
- Negative likelihood 를 최소화 = log Negative likelihood 를 최소화
모두 동일한 의미이다.
Multiclass
Multiclass classification의 경우에는 출력층 활성화 함수로 softmax를 사용한다.
sigmoid는 이진 분류의 확률만 반환해주는 반면, softmax는 다범주의 확률 값을 반환할 수 있기 때문이다.
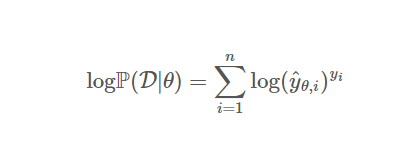
위의 식은 log likelihood의 식을 일반화 한 식이다.
여기서 주의할 점은 y(i)가 지수 함수의 제곱의 역할이 아니라 index로 바뀐다. 즉, True label과 관련된 확률 값만 보겠다는 뜻이다.

영상을 보면 이해가 쉽다.
구현을 보면, softmax로 확률값으로 변환된 값 중 정답 index에 해당되는 부분을 매핑하는 것을 알 수 있다.
| Cross - Entropy |
Negative log likelihood loss와 수식이 비슷하나, 개념이 다르다.
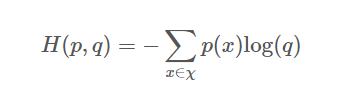
Cross - Entropy는 두 확률 분포 사이의 거리를 구하는 것이다. p를 정답 분포, q를 예측 값의 분포로 본다.
구현할 때, y의 정답 분포를 원핫 인코딩시켜 0,1의 원소로 만든다. 정보이론의 관점이다.
ex) y(i) = 2, y_pred(i) = [0.1, 0.2, 0.7]의 경우
y(i) = [0, 0, 1]로 변환한다.
변환 한 값을 보면 결국 y(i)는 2인 확률이 1인 확률 분포가 되고, 그것을 이용하여 분포의 거리를 최소화 시키는 개념이다.
결론
1. Negative log likelihood loss: 확률론적 관점(데이터에 가장 잘맞는 파라미터의 값을 예측)
Cross-Entropy: 정보 이론의 접근, 두 확률 분포의 거리 관점
2. pytorch
2-1. CrossEntropyLoss 안에서 LogSoftmax와 Negative Log-likelihood 가 진행되기 때문에 softmax나 log 함수가 적용되지 않은 모델 output(raw data)을 input으로 준다.
2-2. NLLOSS(Negative log likelihood loss)에서는 input에 logsoftmax를 먼저 적용해야한다.
다음 시간에는 MAE, MSE, RMSE 차이와 언제 사용하는지에 대한 포스팅으로 이루어지겠다.
이번 학습을 하면서, 수학적인 개념이 많이 등장해 당황스럽고 이해하기 어려웠다.
마무리하며
- 손실함수에 대해 알았고, 경사하강법 중에 미분을 통해 최소값을 구할때 local maximum의 문제는 어떻게 해결할까?
- 그리고 Cross-Entropy의 개념이 왜 정보이론의 개념이고, 그것이 두 확률 분포의 사이를 대신할 수 있는 이유는 무엇일까?
- log를 사용하면 큰값의 영향력은 줄고(첨도와 왜도) 완만한 그래프가 되는데, 계산의 편의성을 위해 log를 사용해도 데이터의 변환이 일어나지 않는가?
참고자료
[ Loss ] Cross-Entropy, Negative Log-Likelihood 내용 정리! ( + Pytorch Code )
[ Loss ] Cross-Entropy, Negative Log-Likelihood 내용 정리! ( + Pytorch Code ) [ Pytorch ] 파이토치 설치하기 [ Pytorch ] 파이토치 설치하기 머신러닝에서 tensorflow와 pytorch는 양대 산맥이죠 pytorch를 설치해봅시다. htt
supermemi.tistory.com
https://ratsgo.github.io/deep%20learning/2017/09/24/loss/
https://angeloyeo.github.io/2020/07/17/MLE.html
최대우도법(MLE) - 공돌이의 수학정리노트 (Angelo's Math Notes)
angeloyeo.github.io
+유튜브 강의 자료 참고
'딥러닝' 카테고리의 다른 글
| Difference of data sampling method (mini batch vs bagging model) (0) | 2023.07.12 |
|---|---|
| Loss function 정리(MAE, MSE, RMSE) (0) | 2023.07.12 |
| 밑바닥부터 시작하는 딥러닝1 (neural network) #part3-1 (0) | 2023.06.27 |
| perceptron (XOR 게이트) Question 해결 (0) | 2023.06.26 |
| 밑바닥부터 시작하는 딥러닝1 (perceptron) #part2-2 (0) | 2023.06.18 |