이번 시간에는 3장 '신경망'에 대해 설명하겠다.
이번 시간에는 활성화 함수와 행렬을 이용한 신경망 구현에 대해 집중 탐구할 생각이다.
신경망 구현은 다음 시간에 설명하겠다.
목차
- 활성화 함수
- 신경망에 행렬
- 출력층 설계
크게 보면 목차는 이렇다. 먼저 '활성화 함수' 부터 공부 시작하겠다.
| 활성화 함수 |
1. h(x)의 이해

이전 퍼셉트론 관점에서 b(편향)을 명시했다. (1*b)
편향도 가중치 관점에서 편향의 입력신호는 항상 1이기 때문이다.
이런 방식으로 명시한 이유는 행렬의 곱과 덧셈으로 신경망 구현을 편리하게 하기 위해서이다.
2. 활성화 함수
활성화 함수로 설명할 함수는 '계단 함수', '시그모이드 함수', 'ReLU 함수' 이렇게 3가지가 있다.
뒤에서 출력층에 사용하는 함수로 '소프트맥스' 함수를 추가로 사용하기도 한다.
계단함수

계단 함수(Heaviside): 극단적 (모 아니면 도)
앞에서 구한 가중치의 합과 편향이 h(x) (계단함수)의 새로운 변수 x값이 된다.
x (b+ w1x1 + w2x2) > 0 이상일 시 출력 1
x (b+ w1x1 + w2x2) <= 0 이상일 시 출력 0
즉, 앞서 구한 퍼셉트론의 구조식 b+ w1x1 + w2x2의 합이 Heviside(계단 함수)의 새로운 x인자가 되는 것이다.
가중치의 가중합이 0이상이면 출력을 1로 하고, 0이하면 출력을 0으로 하는 구조이다.
->그렇다면 이런 활성화 함수는 왜 사용하는 것일까?
그전 활성화 함수가 무엇인지 알아보자

활성화 함수는 입력값의 가중합의 신호를 출력 값의 맞게 분류하려고 사용한다.
즉,

입력신호에 따라 발생하는 가중합은 가능한 경우의 수가 inf이다. 실수 전체가 가능하다는 뜻이다.
이러한 값으로는 인공 신경망을 사용하는 의미가 없다. 학습을 통해 적절값으로 분류 할 수가 없기 때문이다.

따라서
1. 가중합 a를 구하고
2. 총합(a)를 활성화 함수에 넣는다.
3. h(a)의 결과를 도출하는 방식이다.
다시 계단 함수를 봐보자

보면 if else 구조인 것을 알 수 있다.
if x인자 음수 -> 0
if x인자 양수 -> 1
이러한 구조는 다층 퍼셉트론 보다는 단층 퍼셉트론에서 많이 쓰인다. (학습할때 미분을 통해 학습하기 때문.)
아직 학습에 대해 배우지 않아서 자세한 부가 설명을 하진 않겠지만, 계단 함수 그래프를 보면 x축에 평행한 직선이다. 미분 값은 그래프에 접선이므로 계단 함수에서는 학습을 위한 미분이 효과가 없다. (전부 0)

추가로 정리한 내용이다. 전기 신호로 보면, 스위치 on, off의 효과와 같다.
시그모이드 함수(sigmoid)
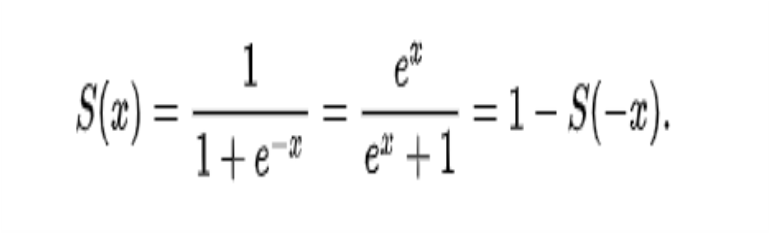
h(x) = 1/ 1 + exp(-x)
수식으로 정리하면 다음과 같다. 여기서 e는 자연 상수로 (2.7182)의 값을 갖는다.
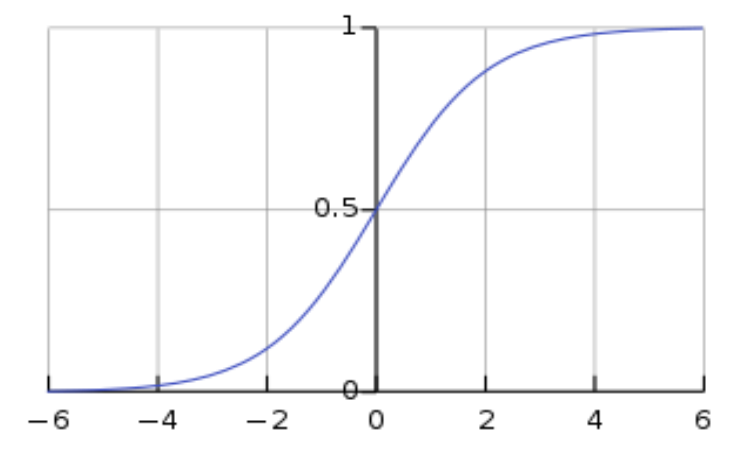
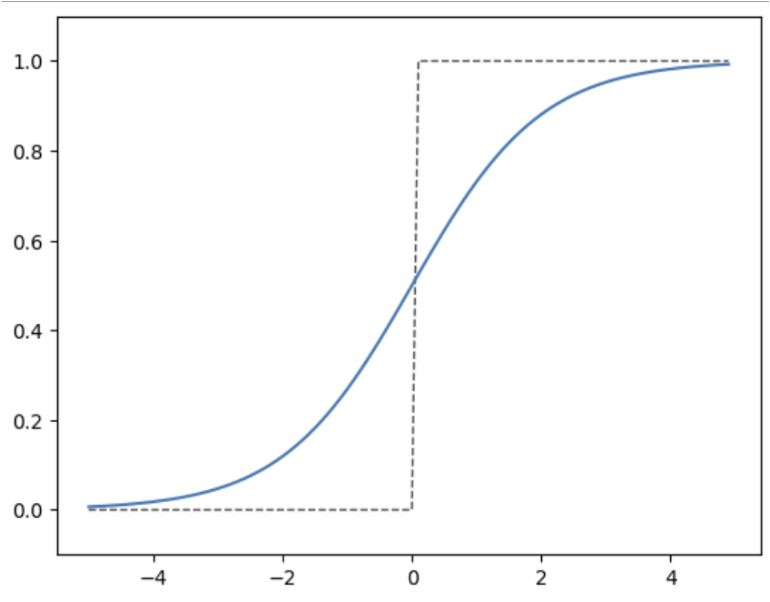
그래프는 이런 모양이 나온다. y값의 범위는 0~1까지의 값만 출력이 가능하다.

시그모이드는 계단 함수의 끊어진 철사 부분을 부드럽게 연결한 모양과 같다. (미분)
사용 이유는 2가지로 요약할 수 있다.
1. 미분의 사용
2. 계단 함수보다 정보 보존(계단: 0~1값 변화하는 부분이 극단적, but 시그모이드는 연속성)
따라서 이러한 특징 때문에 일반적으로
다층 퍼셉트론: 시그모이드
단층 퍼셉트론: 계단 함수
이렇게 주로 사용한다.
cf. 시그모이드 함수의 그래프 그리는 법
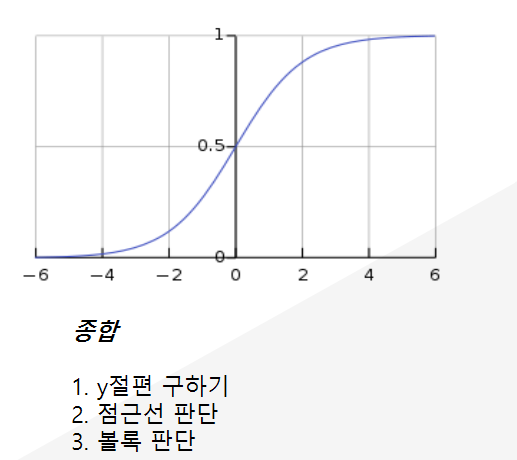
3가지로 구할 수 있다.
1. y절편 -> x에 0을 대입하면 1/2이 된다.
2. 점근선 판단 x를 lim->inf와 lim -> -ing로 보내보면, 양의 무한일땐 1, 음의 무한일땐 0에 수렴한다.
3. 볼록 판단
이건 2번 미분해야한다. 고등학교 수학시간에 구한적이 많을 것이다. 볼록 판단과 함께 최대 최소 구할때도 사용한 방식인데 따로 구하지는 않겠다.
3. python 활성화 함수 구현하기
계단함수
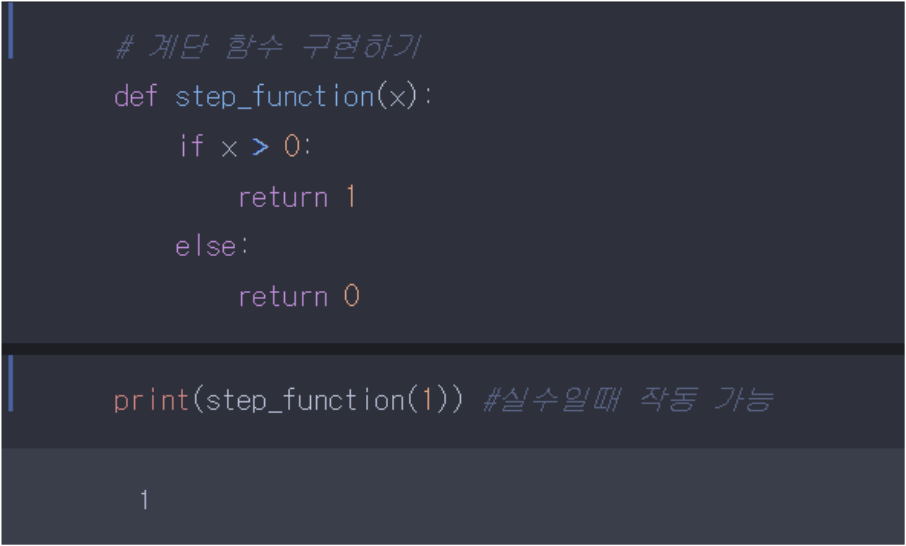
if else코드이니 따로 설명하지 않겠다.
하지만 x값에 실수가 아닌 행렬을 대입할때는 오류가 발생한다.
그 이유가 무엇이냐면,
행렬이 0보다 크다 작다?
말이 안됨 how?해결(실수일때 사용 가능)
따라서 위의 코드를 행렬에서도 구현 가능하려면, numpy의 트릭을 이용 해야한다.


y = x>0에 행렬값을 넣으면 각 원소마다 불린 어레이을 반환한다. 맞는 조건이면 True 아니면, False를 반환한다.
True와 False에 astype(np.int)함수로 변형 시켜버리면 불린값이 숫자로 반환된다. 구현하려는 방식과 동일하다.
pyplot의 구현 방식
pyplot의 구현 방식에 대해 알아보자.
공부하면서 이상한 부분을 못느꼈는가?
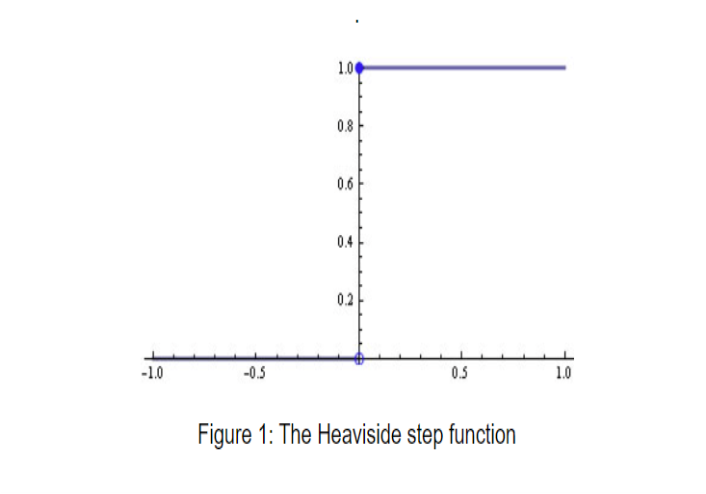
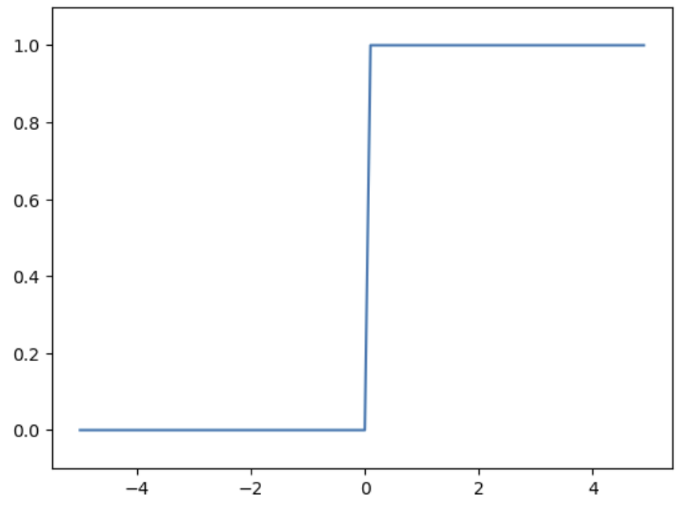
밑과 위와 그래프가 같아야하는데, 다르다. 실제 함수 그래프에서는 끊어져 있어야 하는 0~1 부분이 파이썬에서는 연결 돼 있다.
Question
x가 0일때 파이썬 시각화 그림은 선이 연결 돼 있음 왜 그럴까?
Solution
python 그래프 그릴때
1. x, y의 값에 따른 점을 찍는다.
2. 그 점을 연결하는 직선을 그린다.
의 방식이어서 그렇다. 먼저 x의 값에 따른 점을 찍고 그리는 방식을 이용한다.
시그모이드 함수로 이해를 구체화 시켜보자
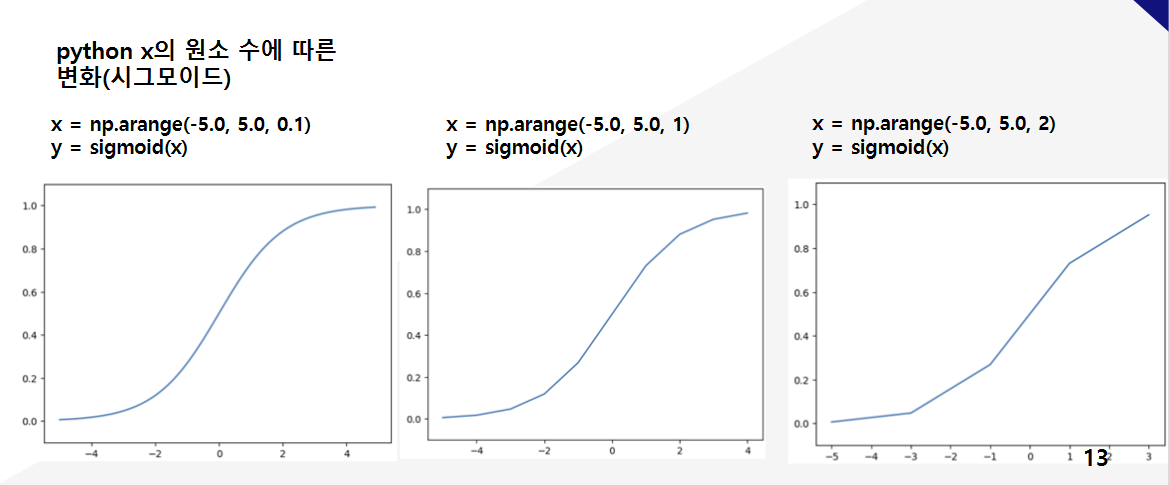
그래프의 구현 방식 때문에, 이런 문제가 발생한다. 적게 찍으면, 찍은 점들을 일자로 연결하기 때문에 어색한 그래프가 나올 수도 있다.
4. python의 브로드 캐스트
파이썬을 구현하다 보면, 행렬 관점에서는 말도 안되는 계산을 해준다.
그 이유는 바로 파이썬의 '브로드 캐스트'기능 때문이다.
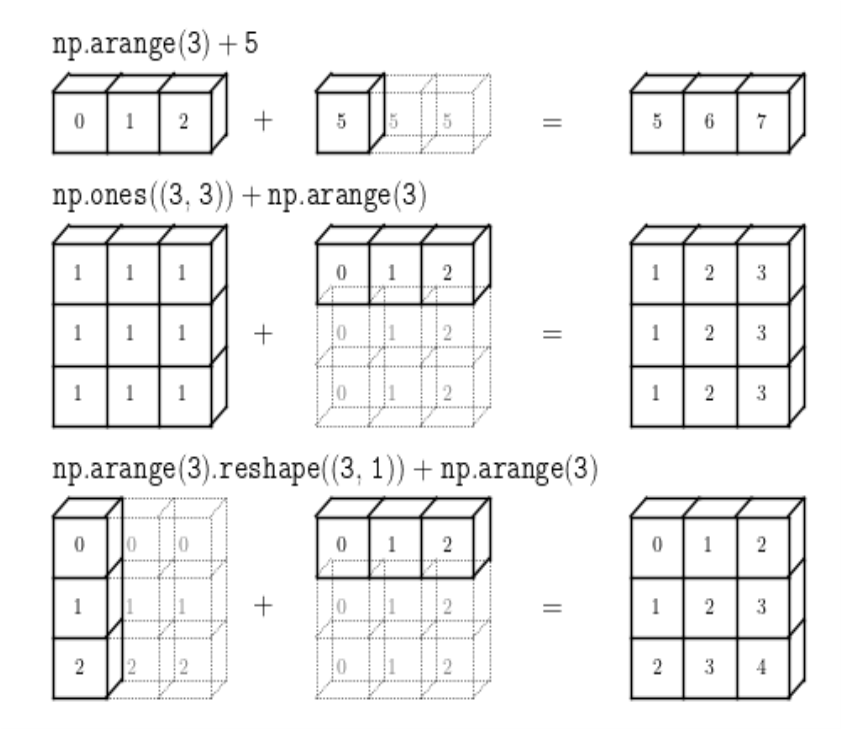
쉽게 요약하면 같은 행렬이 되도록 행렬을 복사하는 것이다. 그림의 예시를 보면 더욱 쉽게 이해할 수 있다.
이러한 파이썬의 장점 때문에 시그모이드 구현 식도 행렬로 계산할 수 있다.

행렬에 관점에선 말도 안되는 계산이다. x의 인자에 행렬이 들어갈 수가 없다. 하지만, 파이썬의 브로드 캐스트 때문에
하나의 수식을 병렬 처리 해준다.
시그모이드와 계단 함수
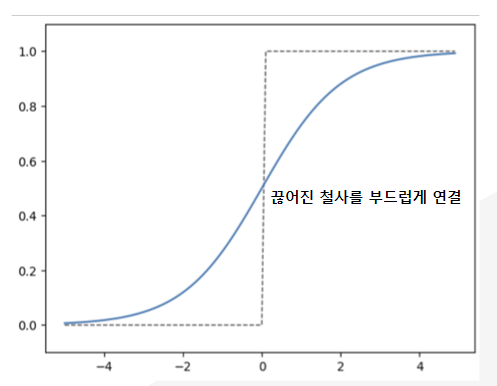
공통점과 차이점을 알아보자.
공통점: 입력이 작을 때 -> 출력 0에 가까움
입력이 클 때 -> 출력 1에 가까움
즉, 중요도에 따라 출력하는 값 0~1
차이점: 매끄러움
계단 함수 0 or 1 반환
시그모이드 함수 : 0~1사이 연속적인 실수 값 반환
5. 비선형 함수
앞에서 본 시그모이드, 계단 함수는 비선형 함수이다. 그렇다면 무엇을 비선형 함수라고 하는 것일까?
Definition
선형이 아닌 함수
선형 함수 : 입력했을 때 출력이 상수배 만큼 변하는 함수
ex) y = c^3 * x
즉, 상수배로 표현할 수 없는 함수
즉 y= ax + b로 표현할 수 없는 함수들을 말한다.
Why?
비선형 함수 사용 이유: 신경망의 층을 깊게 하는 의미가 없어짐. ->
선형 함수를 사용해서는 안됨.
층을 쌓지 않아도 직선으로 표현되면, 층을 쌓는 것이 비효율적 연산 속도만 잡는다. (층을 아무리 쌓아도 은닉층이 없는 네트워크와 동일하다.)
Example
y = c^3 * x 이것도 결국 y= ax + b로 표현가능
h(h(h(x))) = c * c * c * x처럼 곱 세번 -> 3층으로 층 쌓음, 활성화 함수 3번 but, 출력 값은 선형 함수 -> 층을 쌓은 의미가 없다.
a = c^3으로 표현 가능
공부하면서 알게 됐는데, Y = aX^이런 것도 비선형이다.(이전까지 기본 1차 2차 3차.. 방정식들은 선형 함수인지 알았다.)
ReLU 함수의 등장
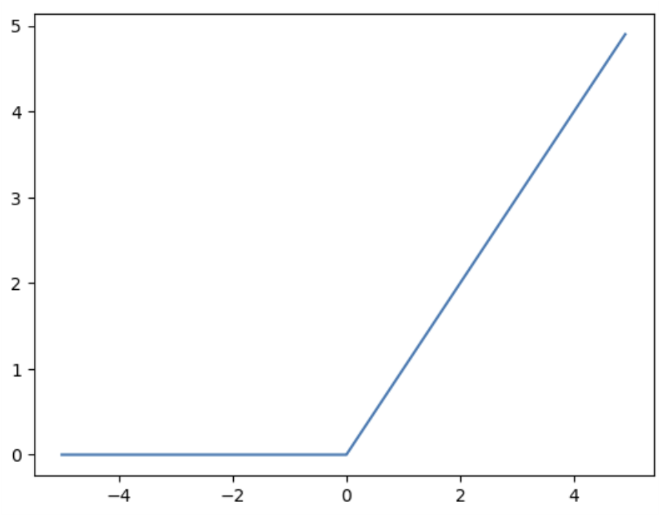
입력이 0 이상 -> 항등 함수
입력이 0 이하 -> 0반환
수식으로 구현해보면
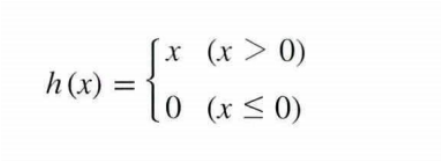
시그모이드 대신에 사용된다고 한다. (기울기 소실 문제 해결)
기울기 소실 문제는 나중에 다시 설명하겠다.
마무리하며
지금까지, 3장 neural network 중 활성화 함수에 대한 파트를 공부했다.
공부하면서,
1. 출력층의 소프트 맥스 함수를 사용하는 이유는?
(이미 시그모이드 함수를 사용해서 확률값으로 반환 되고, 입력 값도 0이상인데 왜 사용할까)
2. 학습할때 미분을 통해 학습하는데, 오차를 줄이는 방향으로 학습 아닌가?, 계단 함수도 미분 가능
학습하는 방법
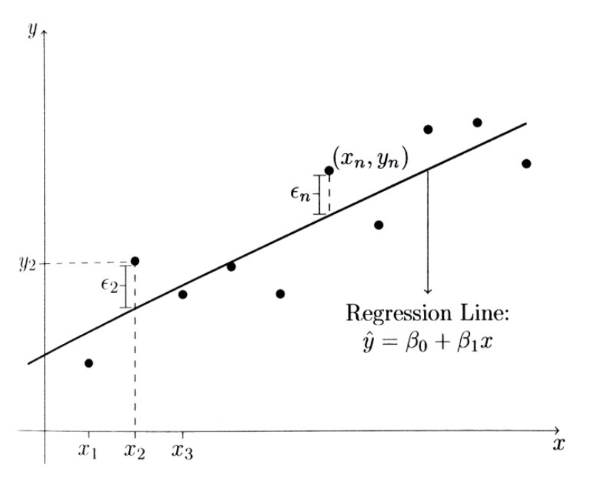
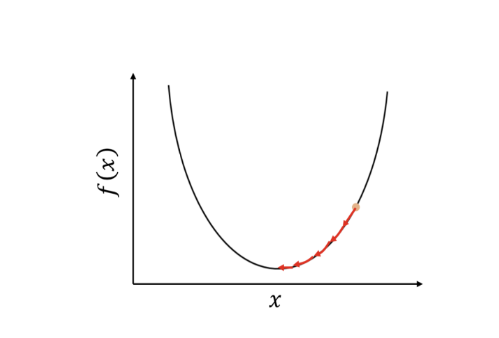
학습할때 오차를 줄이는 방향으로 경사하강법 사용한다고 했는데(머신러닝 회귀파트)
계단 함수도 오차의 제곱의 값 여러 개의 분포를 발생할 수 있지 않을까?
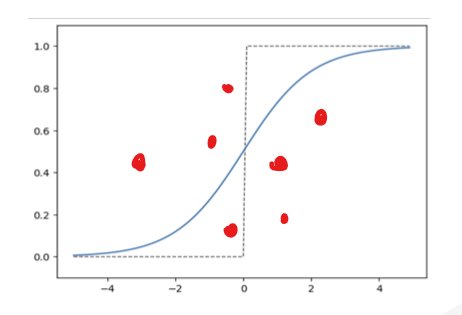
실제 값과 계단 함수로 구현한 값의 오차의 제곱의 분포는 위의 그래프와 같이 2차식을 만족할 거 같다.
WHY? (오차 - 계단함수)^2 구현 값은 거리 차이 때문에, 다 다를거 같은데?
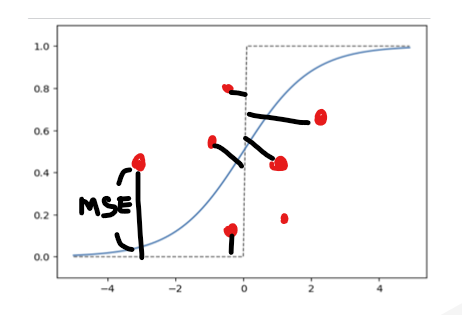
왜 굳이 시그모이드 함수를 사용하는지..
궁금해졌다.
3. 재밌다. 아직까진 쉬워서 그런지 몰라도 코드와 이론을 함께 배우니 재밌는거 같다.
'딥러닝' 카테고리의 다른 글
| Loss function 정리(MAE, MSE, RMSE) (0) | 2023.07.12 |
|---|---|
| Loss function 정리 (Cross entropy, Negative log likelihood) (1) | 2023.07.10 |
| perceptron (XOR 게이트) Question 해결 (0) | 2023.06.26 |
| 밑바닥부터 시작하는 딥러닝1 (perceptron) #part2-2 (0) | 2023.06.18 |
| 밑바닥부터 시작하는 딥러닝1 (perceptron) #part 2-1 (3) | 2023.06.18 |