저번 주부터 과외를 받기 시작했다. 데이터 분석을 공부하다가, 모르는 부분을 같은 과 선배에게 끊임 없이 물어봤었는데, 형이 과외 받으라고 해서 과외를 받기 시작했다.

과외 방식은 주어진 분량까지 발표할 자료를 혼자 스스로 준비하고 파워포인트와 주피터 노트북으로 발표하는 형식이다. 그 중 이번주는 2장 퍼셉트론까지 준비했다. 준비하면서 알게 된 부분을 이번 시간을 통해 공유하려고 한다. 책의 내용을 기반으로 설명하겠지만, 내가 스스로 느낀 부분 위주로 설명할 생각이다.
그럼 시작해보자.
밑바닥 부터 시작하는 딥러닝1 perceptron #2 start

목차
1. 단층 퍼셉트론의 이해
- 퍼셉트론의 이해
- 신경계, 인공 신경망
- 일차 함수 관점
2. 퍼셉트론의 논리회로
- 단층 퍼셉트론의 논리회로(AND, NAND, OR 게이트)
- 부등식 영역 관점
- 코드로 확인하기
3. 다층 퍼셉트론의 등장(퍼셉트론의 한계)
- 다층 퍼셉트론의 등장
- XOR 게이트의 이해
cf. 내가 만든 ppt와 함께 공부하면, 이해가 더 잘될 것이다.
| 1. 단층 퍼셉트론의 이해 |
신경계와 인공 신경망

perceptron은 인간의 신경계를 모방한 것이다. 총 3부분을 모방했는데 살펴보면,
1. 시냅스 : 전기 신호 조정(가중치 곱함)
2. 소마 : 가중치와 곱을 더해줌
3. 전달 시: 가중치의 합이 특정 임계값을 넘겨야 전달 가능
인간의 신경계 이 3단계 모방했다고 할 수 있다.

퍼셉트론은 3단계와 함께 다수의 신호(input)을 입력받아 활성화 함수를 통해 하나의 신호로 나오는 것을 말한다. 머신러닝의 대표적인 방법 중 하나이고, 이번 파트에서는 직접적인 코드 구현보다는 numpy를 이용하여, 기본적인 구조를 아는 시간이 될 것 같다.

직접 만든 ppt자료를 쓰겠다. x1, x2는 입력 신호로 주어지는 값에 따라 다르다. 입력신호의 가중치를 곱하고, 그것의 합이 특정 임계값을 넘어야 1(전류가 흐른다)로 출력되고, 만족하지 않을 시 0(전류가 흐르지 않는다)로 출력 되는 구조이다.

작동 원리가 전기 회로와 유사하다고 할 수 있다. 전기가 흐를때 저항을 만나면 전류 세기가 달라지는 것처럼, 가중치를 통해 x1, x2의 입력받은 값의 세기를 조절한다. 중요한 값일수록 가중치를 높게 하는 것이 좋다. 그래야 출력이 잘되기 때문이다.
학습 Point
지금부터는 내가 이해한 방향으로 설명하겠다. 쉽게 이해하도록 나만의 방식으로 정리했으니 참고하면 좋을 것이다.

이해한 방향
x: 변수
입력값이 무엇인지에 따라 변하는값
w, θ : 입력 파라미터
값을 직접 정해야 하는 것
가중치와 임계값은 주어지는 논리회로나
문제를 보고 적절한 값을 직접 정해야한다.
두 값에 따라 그래프의 모양이 정해진다.
(심층 신경망에선 아님)
우리가 프로그래밍으로 모델링을 할때 적절 파라미터를 넣는다. 단층 퍼셉트론에서도 모델링을 할때 w,θ 값이 가장 중요하다. 이것에 따라 출력될 값들이 달라지기 때문이다. 자세한 내용은 일차함수 관점에서 설명할때 자세히 설명하겠다.
일차함수 관점(퍼셉트론 일차함수로 보기)
먼저 일차함수에 대해 복습하는 시간을 갖겠다.
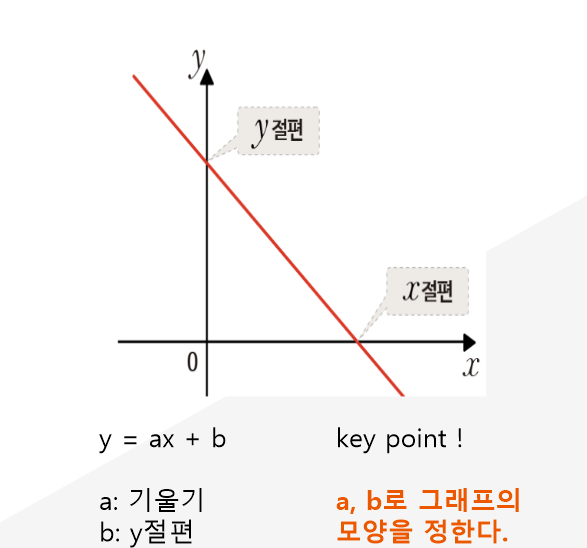
대표적인 일차함수 그래프의 모양이다. 중학교 수학 시간에 배운 것 처럼 a: 기울기, b: y절편이다.
그래프의 모양을 결정하는 중요한 값도 a,b이다. 이것의 모양에 따라 그래프의 모양이 달라진다.
따라서 적절한 일차 함수를 그리려면 a,b의 값을 조정하는 작업이 필요하다.

무슨 의미인지 살펴보면, 퍼셉트론의 구조식도 w2를 y라고 생각하고 이항하면 결국에는 일차함수 구조식과 동일하다는 것이다. 여기서 w(가중치): 기울기, b(-임계값): y절편이 된다는 뜻이다. 즉 w,b로 그래프의 모양이 정해진다.
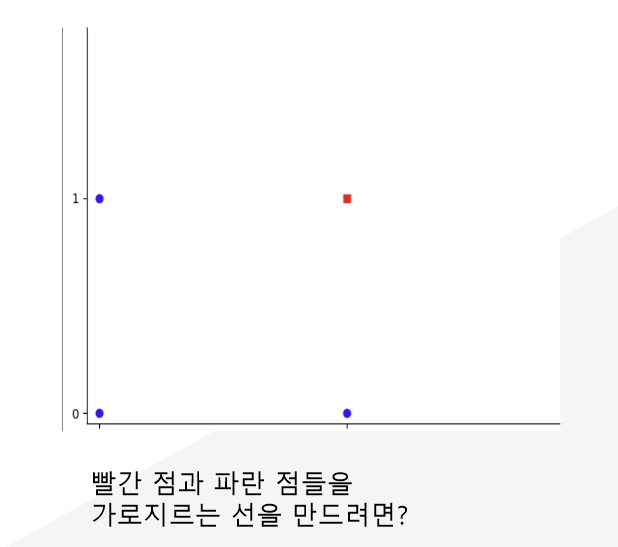
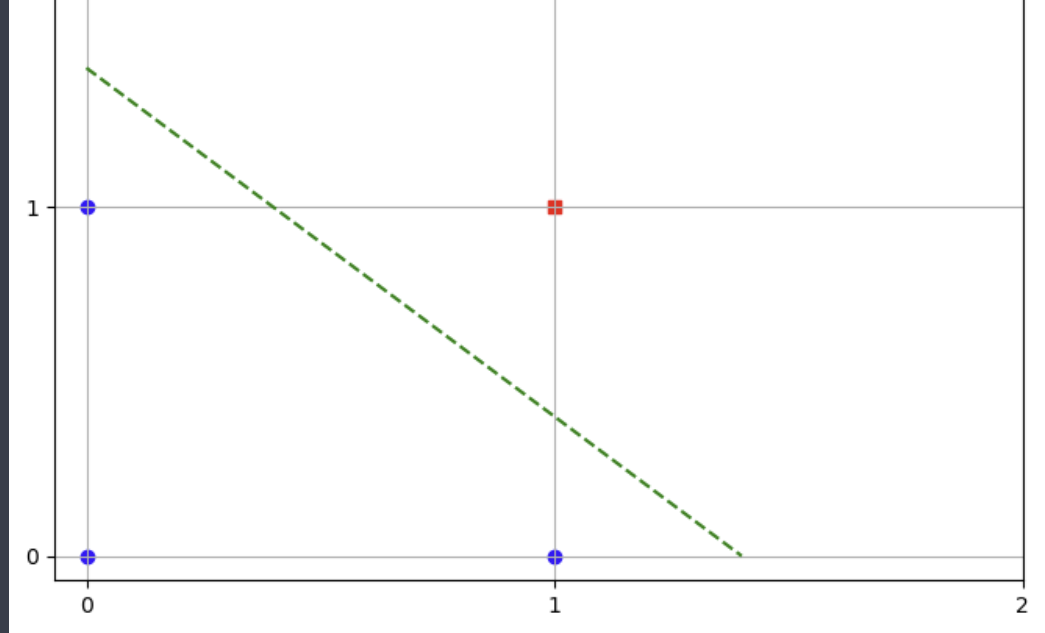
위의 예시는 대표적인 논리회로 중 하나인 AND 게이트이다. 파란점과 빨간 점을 가로지르는 직선을 만드려면 어떻게 해야할까?
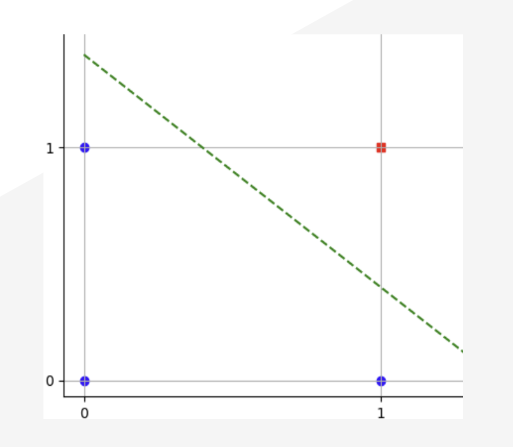
이런식으로 그래프가 그려져야한다. 가능한 그래프의 모양은 수없이 많다. 이것은 단층 퍼셉트론의 관점에서 보면 w, b값을 조정하여 그래프를 그려 조절 가능(핵심) ,가로지르는 선 생성 가능하다는 의미가 된다.
| 2. 퍼셉트론의 논리 회로 |
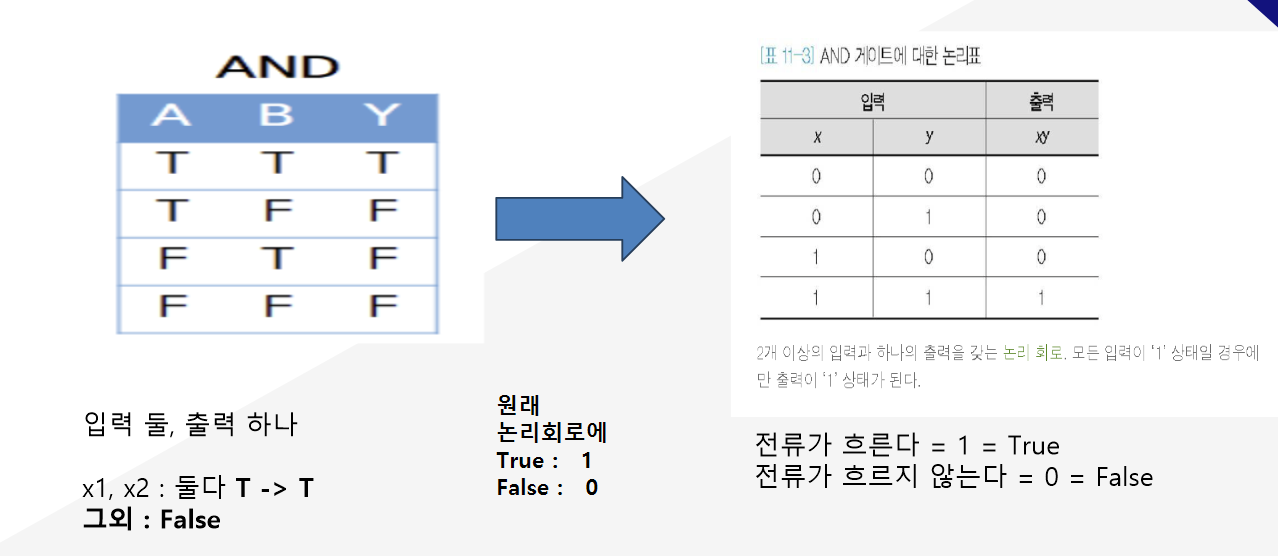
단층 퍼셉트론의 논리회로는 AND, NAND, OR 총 3가지가 있다.
그 중 위의 사진은 AND게이트 사진이다. AND게이트는 입력(X) :2, 출력: 1로 구성돼있다.
기본적인 논리구조로, 입력이 True, True -> True의 구조이다.
이것을 이진법으로 바꾸면
입력이 x1:1, x2:1일때만 출력이 1이 돼야한다. 그 외에는 전부 출력이 0이다.
주어진 논리회로를 만족시키려면 가중치와 임계값은 어떻게 정해야할까?
교제에서는 (0.5, 0.5, 0.8), (0.5, 0.5, 0.7), (1.0, 1.0, 1.0)로 지정되어 있는데, 이것은 어떻게 정해지는걸까?
정답은 부등식의 영역 방법으로 정해진다.(뒤에 설명하겠다.)
NAND 게이트
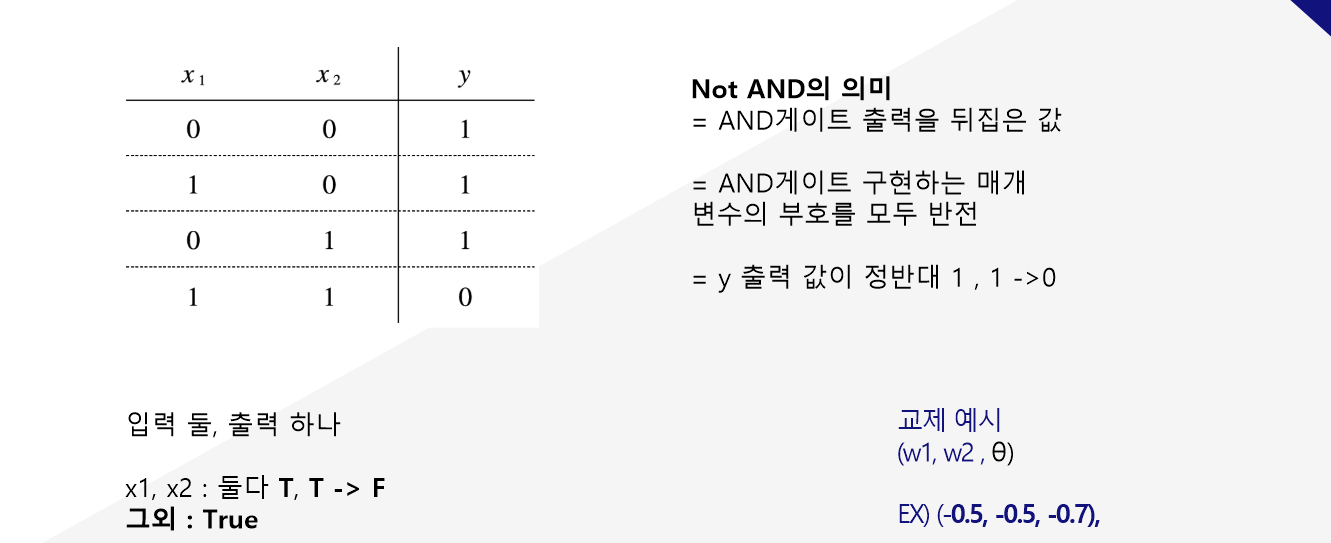
Not AND의 의미이다.
AND게이트와 반대로, 이번에는 True, True -> False의 구조이다.
즉 입력값이 1,1 일때 출력은 0이 된다.
그외에는 전부 1이다.
추가로 AND게이트의 부호를 모두 반전 시키면 Not AND가 되는데, 아까 AND게이트의 가중치와 임계값에서 -1을 곱하면 된다. 교재에서는 (-0.5, -0.5, -0.7)
OR게이트
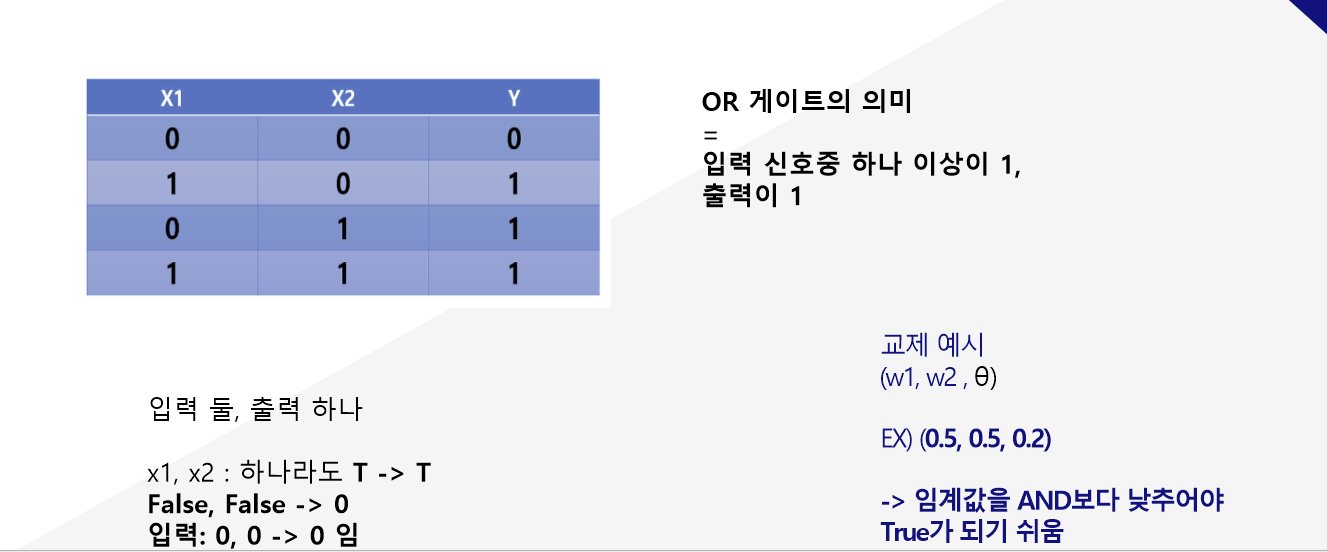
똑같다. 논리 구조는 똑같은데 OR게이트는 입력신호중 하나 이상이 1이면 출력이 1이 되는 구조이다.
교재에서는 예시로 (0.5, 0.5, 0.2)로 두었다. 임계값을 AND보다 낮추어야 한다는데, 그 이유는 무엇일까?
(가중치와 임계값이 어떻게 정해지는 지는 부등식 영역을 설명하면서 알려주겠다.)
부등식 영역
부등식 영역의 기본 개념부터 설명할 것이다.
고등학교 수업시간에 등장한 개념이어서 글 한번 읽어보면 기억이 날 것이다.
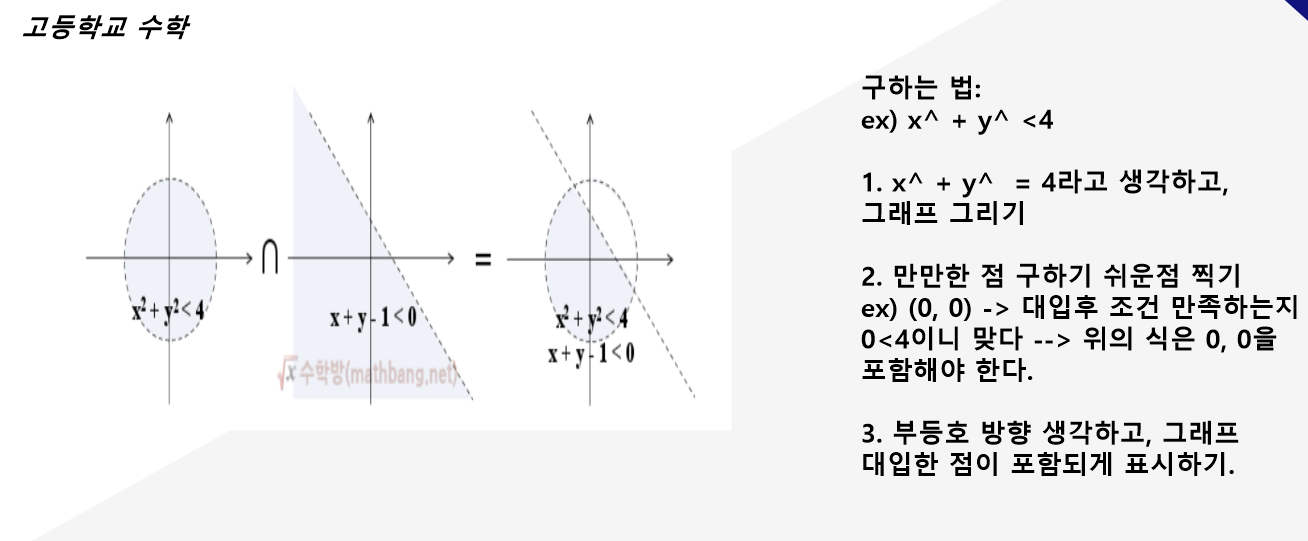
이것을 알아야 가중치와 임계값을 조정하는 이유를 알 수 있다.
요약해서 설명하면
1. 주어진 방정식의 그래프를 그리고
2. 그중 0,0처럼 값을 입력했을때 계산하기 식을 대입하여, 비교한다. 첫번째 그림에선 0,0이 포함되도록 해야하니
0<4의 값이 만족해야한다. x^+y^<4가 돼야한다는 뜻이다(만약 x^+ y^>4이면 바깥쪽 영역을 만족하는 것이다. 0,0을 만족하지 않으니)
3. 주어진 식에 맞게 부등호 방향을 설정
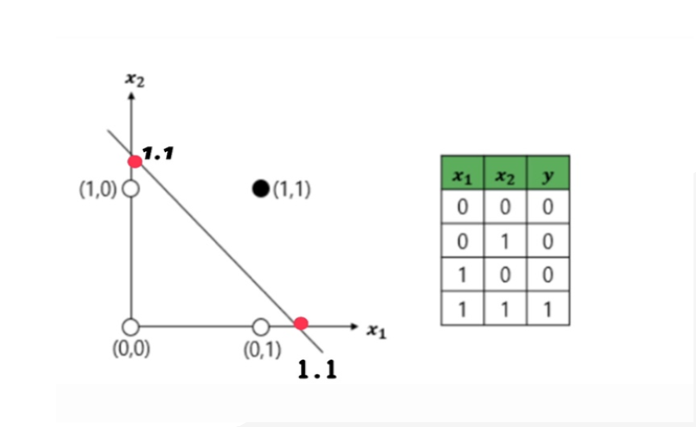
왼쪽 데이터 프레임 AND게이트이니 (1,1)일때 1을 출력할 수 있어야 한다. 그래프는 어떻게 그려야할까?
Description
1. 예제에서 나온 W, θ 말고 셀수없는 선 가능
2. 어떤 점도 가능하니 예시로 x절편 1.1, y절편 1.1인 일차함수 기준으로 설명하겠다.
Soultion
1. 그래프 찾고 그리기
x1 절편 :1.1, x2 절편: 1.1
-> x1/1.1 + x2/1.1 =1 (공식)
2. (0, 0) 만만한 점 넣어보기
0, 0 넣었을 때, 0, 0은 진리표에서 출력x 따라서 포함되면 안됨-> x1/1.1 + x2/1.1 > 1
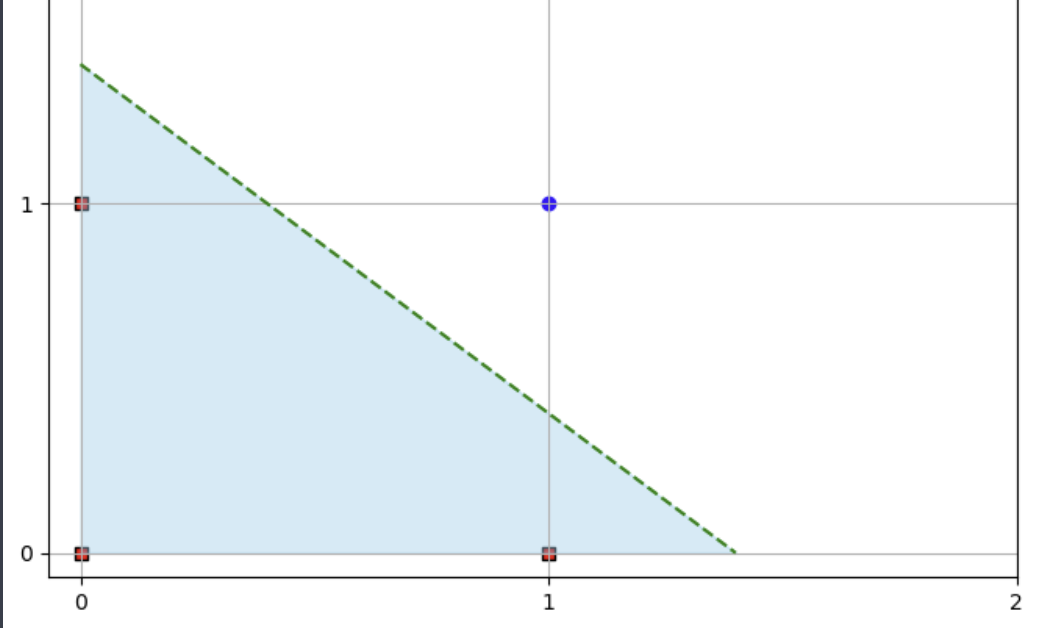
3. 그래프 확인하고 영역 그리기
이런식으로 1,1을 입력값으로 넣었을때 출력이 1이 되려면 W, θ을 적정 조정해서 먼저 그래프의 모양을 잡아야한다(그래프가 주어진 점을 통과하도록)
그 이후 1,1부분이 출력 되려면 일차 함수 기준 그래프를 그렸을때 위쪽 부분의 영역이 출력 돼야한다는 것을 의미한다.
이것은 부등식의 영역을 구하는 방법으로 정해지며, 그것에 따라 W, θ의 적정 값과, 부등호의 방향을 결정할 수 있다.
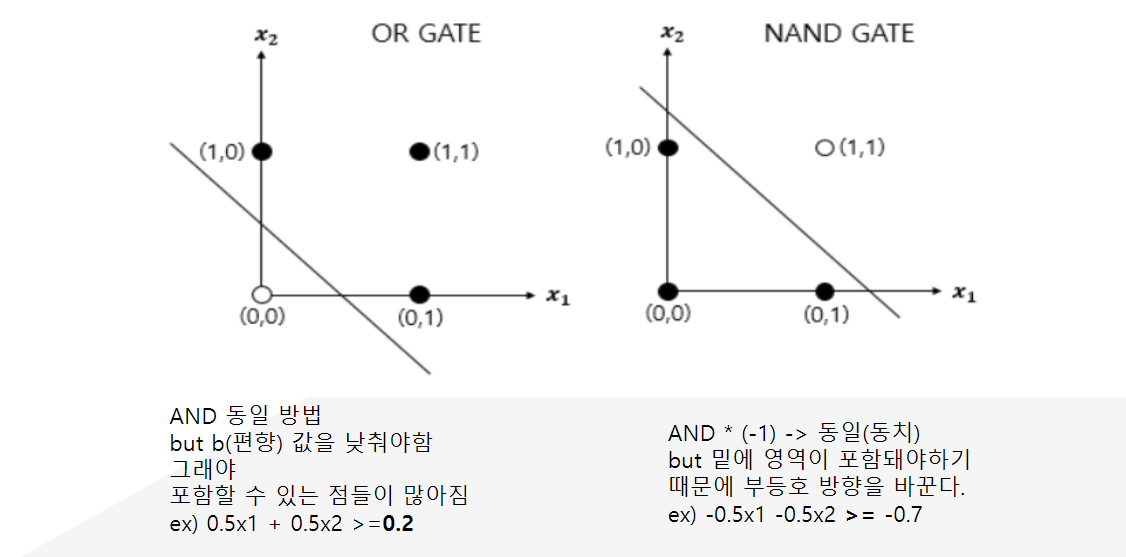
OR과 NAND도 똑같다. NAND는 AND게이트에서 -1을 곱한거 뿐이니 값은 똑같은데, 밑에 부분에 영역이 출력 돼야한다.
그러려면 부등호의 방향을 바꿔야 밑에 부분이 출력된다.
OR은 AND게이트보다 더 많은 값을 출력해야한다. 그러려면 y절편 즉, AND게이트보다 b(편향)값을 낮춰야 가능하기 때문에 아까 θ값을 0.7(AND)->0.2(OR)로 줄인 것이다.그래야 출력 될 수 있는 입력 값의 범위가 넓어지니 말이다.
코드로 살펴보자.
AND

너무 쉬운 코드이고, 앞에서 설명한 그대로 하면 된다.
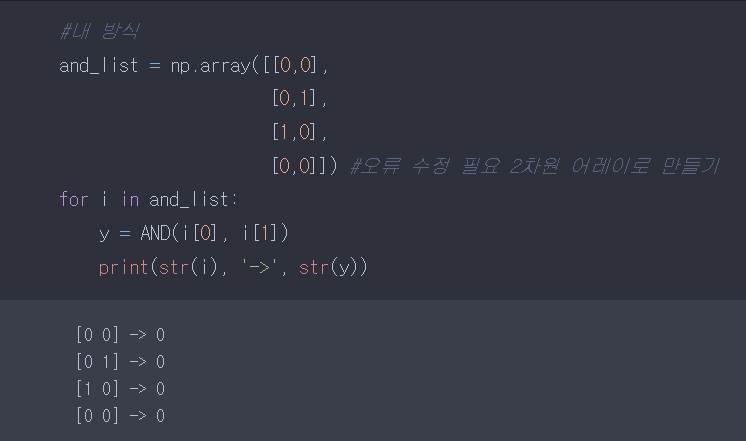
넘파이 팬시 인덱싱을 이용하여 입력값과 출력값을 보기 좋게 표현해봤다.
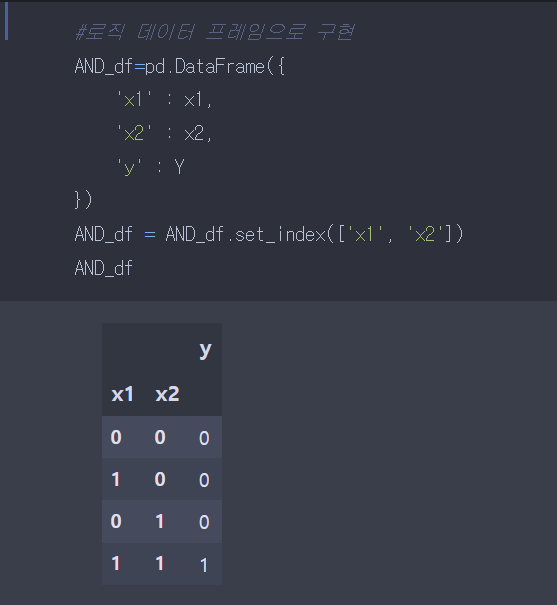
이번에는 논리회로의 진리표를 데이터 프레임으로 표현해봤다.
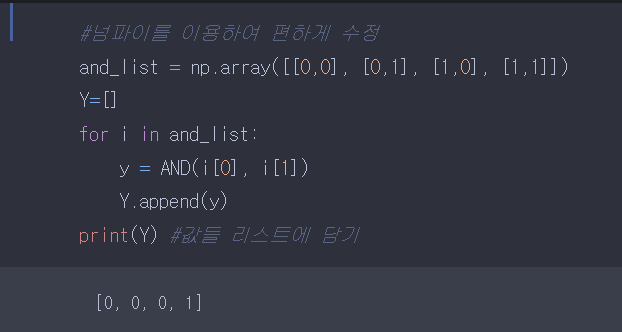
y값을 리스트에 담았다.
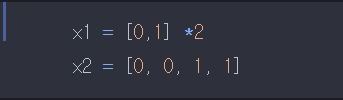
입력값을 리스트 형태로 정의해봤다.

그래프를 그리려고 시각화 코드를 직접 짜봤다.
NAND, OR

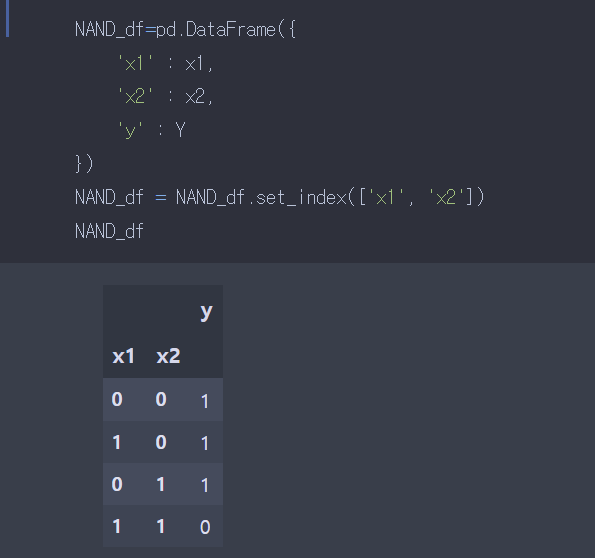
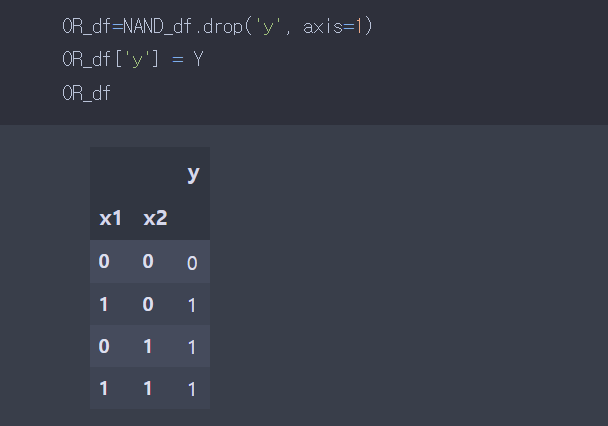
아까와 동일한 방식으로 진리표를 만들었다.
똑같이 시각화 코드를 작성하고 이번에는 범위까지 출력해보았다.
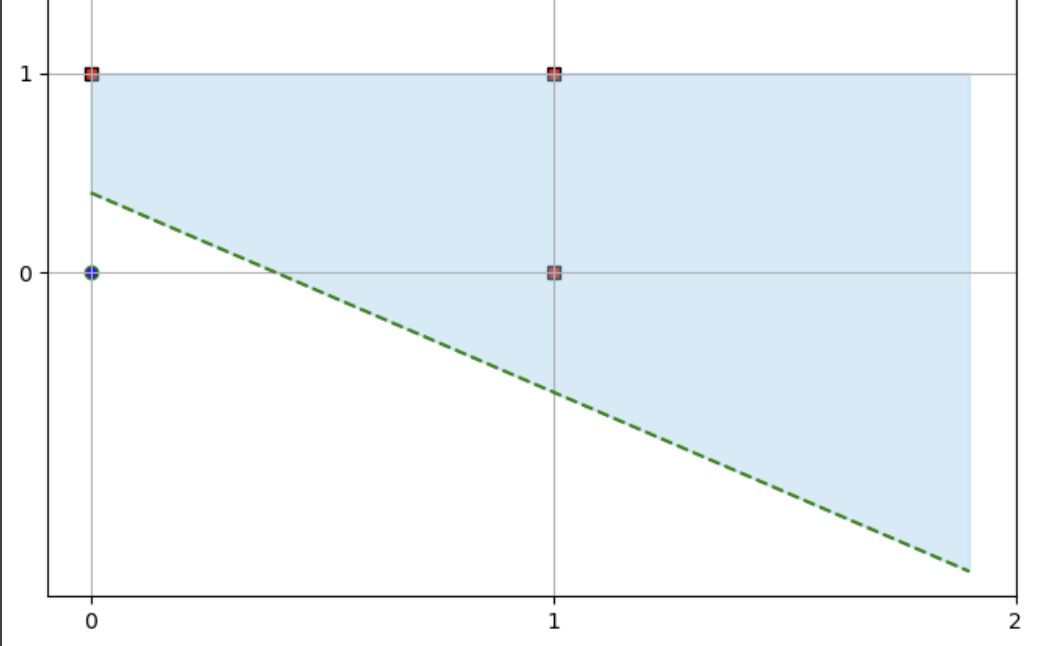
plt.fill_between라는 함수를 이용하여 범위를 나타나보았다.
내용이 너무 길어져서, 오늘은 여기까지 작성할 것이다.
마무리하며
깨달은 것
1. ADsP 제대로 공부한 거 효과가 있음(인공 신경망이나 기초 통계 지식)
(은닉층의 구성이 어떻게 등)
2. 기초 수학 지식을 복습하며 까먹었던 부분, 기본적인 구조 이해가 잘 됐다.
요즘 ADsP공부를 정말 잘했다라는 생각이 많이 든다. 확실히 전반적인 구성을 보고 공부하는 것이랑 그냥 하는 것이랑은 차이가 많은것 같다. 담번에는 또 새로운 글로 찾아오겠다.
'딥러닝' 카테고리의 다른 글
| Loss function 정리(MAE, MSE, RMSE) (0) | 2023.07.12 |
|---|---|
| Loss function 정리 (Cross entropy, Negative log likelihood) (1) | 2023.07.10 |
| 밑바닥부터 시작하는 딥러닝1 (neural network) #part3-1 (0) | 2023.06.27 |
| perceptron (XOR 게이트) Question 해결 (0) | 2023.06.26 |
| 밑바닥부터 시작하는 딥러닝1 (perceptron) #part2-2 (0) | 2023.06.18 |