오늘도 저번 시간과 동일하게 Loss function을 정리하려고 한다. 저번 시간에는 분류에서 주로 사용되는 Cross - entropy와 Negative log likelihood loss에 대해 배웠다.
cf.
Loss function 정리 (Cross entropy, Negative log likelihood)
오늘은 Loss function에 대하여 학습을 진행할 것이다. Loss function으로 미분이 가능하게 만들어, 학습에 판단 지표로 만든다는 것은 알겠는데, 각각 무슨차이인지 몰랐다. 이번 학습을 통해 조금 더 l
hyeong1197.tistory.com
이번에는 회귀에서 사용되는 MAE(mean absolute error), MSE(mean squared error), RMSE(Root mean squared error)에 대하여 설명하겠다.
목차
- MAE?
- MSE?
- RMSE?
- MAE vs MSE vs RMSE
각 개념을 먼저 설명하고, 차이점을 설명하는 방식으로 서술하려고 한다.
| MAE |

특징:
- 이상치에 민감 X
- 미분 불가능 한 지점 O
- 직관적, but 오차가 음수인지 양수인지(실제가 예측보다 차이가 작은지, 큰지) 판별 불가


Descriiption
MAE는 절대값의 특성 때문에 0인 부분에서 꺾이는 그래프이다. 이런 이유때문에
MSE와 비교했을때, 이상치에 민감하지 않는다(MSE는 민감.)
또한 직선의 0을 기점으로 꺾인 그래프이기 때문에 미분이 불가능한 지점이 있다.
(미분은 순간 변화율, 접선의 개념. 주로 둥근 부분에서 가능하다 like sigmoid)
보다 오차의 값이 정확하게 나오기 때문에 직관적으로 이해 가능하지만, 절대값의 특성 때문에 오차가 음의 오차인지, 양의 오차인지 판별이 불가능하다.

추가로, 일정 거리만큼 이동하기 때문에 최적값의 수렴에 어렵다.
(이 부분은 Gradient와 경사 하강법의 개념을 확실히 이해하고 다시 공부 해야겠다.)
| MSE |

거리의 개념이다. 가장 잘 활용하는 오차 함수이다. 오차의 제곱에 개념이 들어가 있다.
특징
- 이상치에 민감(이상치가 클수록 가중치 증가)
- 전 구간에서 미분이 가능함
- 최적값의 수렴할수록 이동 거리 감소
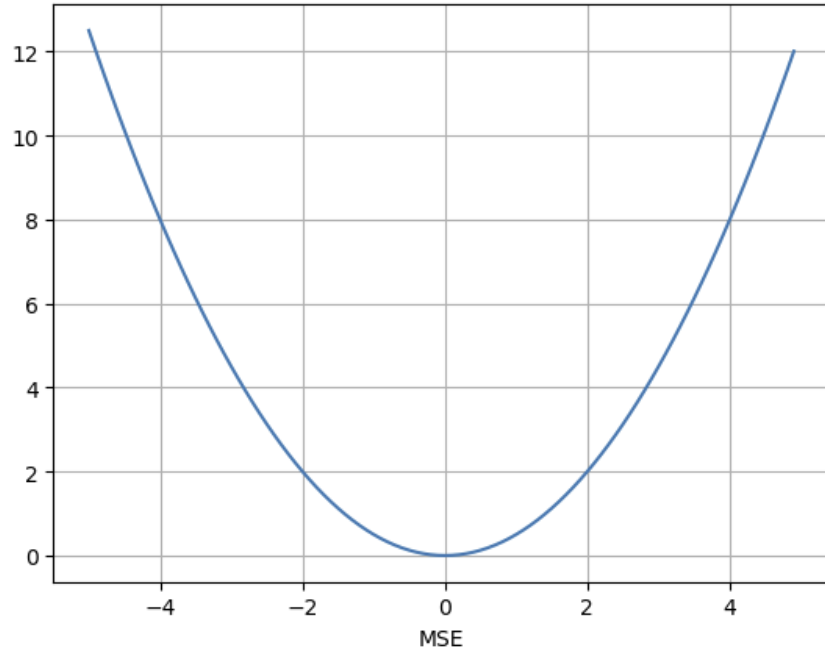
Description
MSE는 2차 함수이다. (떨어진 오차의 제곱을 하기 때문에)
그렇기 때문에 구간별 가중치의 차이가 심하다.(0~1까지의 경우 제곱-> 값이 작아짐, 1이상 -> 가중치가 커져 더 높은 값)
2차 함수의 특성때문에, 전 구간 미분이 가능하다.
또한 가장 많이 사용되는 함수여서 거리의 개념으로 이해하기 쉽고,
최적값의 수렴할수록 이동 거리가 짧아진다.
| RMSE |
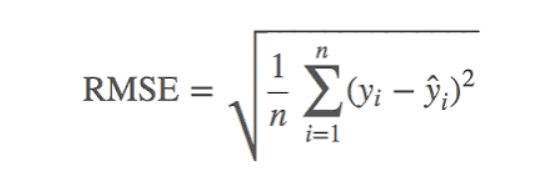
MAE와 MSE의 각 단점을 보완하는 방법이라고 생각하면 된다. MSE에 Root를 사용하는 방식이다.
특징
- MSE의 단점 보완(이상치 민감)
- MAE의 중간 정도 이상치 민감도.
- 미분 불가능한 지점을 갖는다.
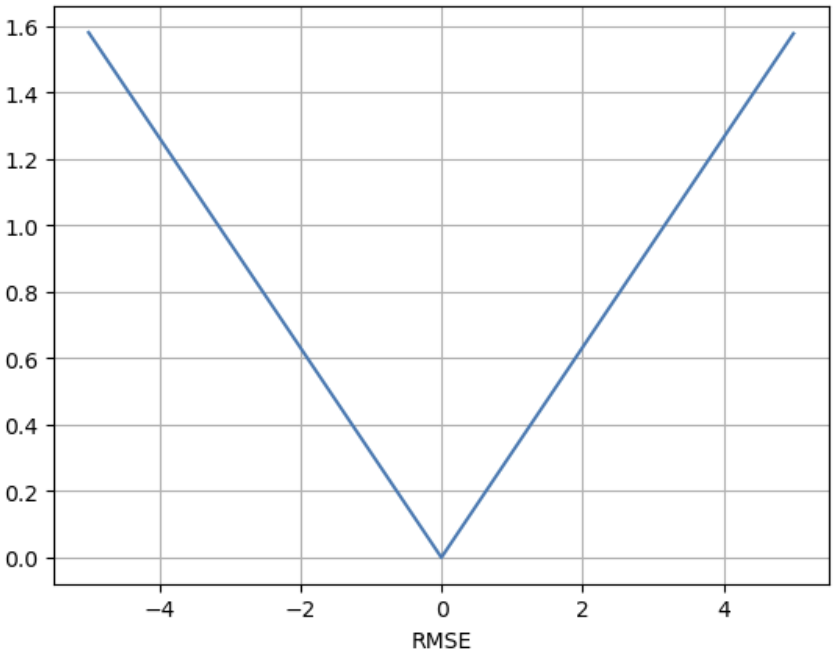
Description
먼저 루트를 이용하여 MSE의 단점인, 이상치에 너무 민감한 부분을 감소 시켜준다.
하지만 이것 또한 제곱을 이용하기 때문에, 이상치에 MSE보다 덜 민감한 정도. MAE보다는 민감.
제곱과 루트의 특성 때문에, 미분이 불가능한 지점이 발생할 수 밖에 없다.
Question
그래프의 모양이나, 제곱한 후 루트를 사용하면 절대값의 오차와 비슷한거 아니냐고 생각할 수 있다.
Answer
실제로 |x| 와 sqrt(x^)은 비슷한 내용이고 둘다 꺾인선 그래프가 나오기 때문이다.
하지만 다른점은 RMSE는 1/n을 사용할때 sprt(1/n)을 사용한다. 즉, total sum한 MSE를 구하고 그 후에 sprt를 적용하는 방식이어서 값이 다를 수 밖에 없고. 그로 인해 MAE보다 조금 더 민감한 이상치의 값을 갖으며, MAE의 단점인 이상치의 똑같은 가중치 적용 문제를 어느정도 해결할 수 있다.
그래서 언제 도대체 이 함수를 사용 해야할까?
MAE: 약간의 이상치가 있는 경우(Overfitting 방지)
MSE: 이상치까지 고려해야 할때.
RMSE: 한쪽에 편향되기 보다 중간의 결과를 얻고 싶을때로 요약할 수 있다.
이상...
마무리하며
1. 왜 분류에서는 정보이론, 회귀에서는 MSE를 주로 사용할까?
2. 이상치에 민감 개념은 생소했는데, 이해하니 재밌다.
3. MSE도 오차가 음인지 양인지 모를 수 있지 않나?(제곱 때문에)
4. 최적값 수렴에 개념 다시 익히자.
5. RMSE가 정밀도의 개념으로 사용할 수 있는 이유?
6. RMSE의 그래프는 어떤 식으로?
7. 여기서 구한 각 오차의 그래프는 무엇을 의미하는지?
'딥러닝' 카테고리의 다른 글
| CNN(Convolutional Neural Network) (1) | 2023.07.31 |
|---|---|
| Difference of data sampling method (mini batch vs bagging model) (0) | 2023.07.12 |
| Loss function 정리 (Cross entropy, Negative log likelihood) (1) | 2023.07.10 |
| 밑바닥부터 시작하는 딥러닝1 (neural network) #part3-1 (0) | 2023.06.27 |
| perceptron (XOR 게이트) Question 해결 (0) | 2023.06.26 |